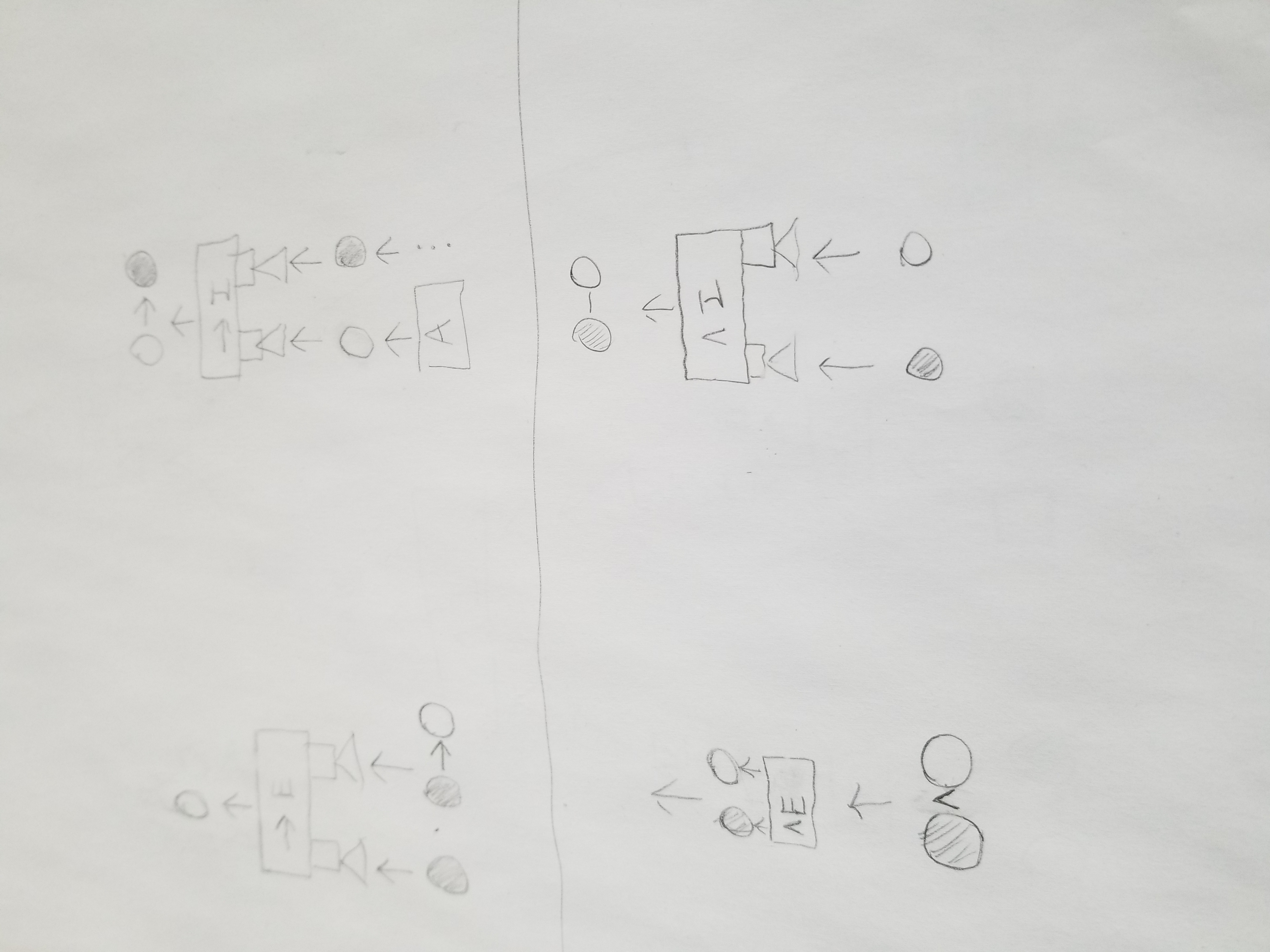
This month, I wanted to make something a little simpler. I'm going to be balancing this month's demo with updating POLYPAINT for an indie game developer showcase in Denver, so I don't want to give myself more than I can handle. I decided to go with a concept I've had in the back of my mind for a while. It's a very abstract game, one that shouldn't require a lot of heavy artwork. The mechanics of the game are really what will sell the concept.
Lewis Carroll was best known for writing Alice's Adventures in Wonderland, but did you know he was also a gifted mathematician? Specifically, he was very interested in symbolic logic, a subject which I have also taken a great interest in. Out of all the people who have written on the subject, I thought Carroll had the most interesting perspective on it.

Symbolic logic is commonly viewed as a tool. It can be used to decide whether or not an argument is valid, it can be used to verify that a mathematical proof is correct, and it can be used to demonstrate that an algorithm for a computer program will produce the expected results. Lewis Carroll, however, thought of symbolic logic as a game. In fact, he wrote a book on the subject (called The Game of Logic). The book came packaged with a board, some counters, and some very fun-to-read instructions (after all, the guy did write Alice's Adventures in Wonderland). A little while ago, I was reading through this book, and I thought about how fun it would be to make a computer game based off the subject of symbolic logic.
I didn't want my game to be a plagarism of Carroll's design, so I got to work on my own. Carroll's game focused more on the use of symbolic logic as a means to the end of validating an argument. The design I came up with is focused on actually proving things.
The rules of the game are pretty simple. It's a puzzle game, with each level consisting of a different puzzle. In each level, you may be given a set of inputs (I say 'may' becuase you might not be given any at all on some levels), and you are expected to produce a clearly telegraphed output. It's an open-ended puzzle game, meaning there are infinitely many valid solutions to each puzzle. The way that you mutate the input(s) into the desired output doesn't matter, as long as you are able to produce the output.
Of course, you aren't free to just transform the inputs any way you like until you reach the desired output. You'll need to follow some rules, and the rules are where the connection to symbolic logic comes in. The rules you are given for manipulating inputs are directly inspired by the rules for proving theorems of symbolic logic.
I know this is getting a bit abstract, so allow me to show what I've been working on so far so you can actually see it in action:
I highly recommend paper prototyping. It can save you a lot of time to plan out (maybe even playtest) the design of your game on paper before you actually start building it. I made some good progress with just paper prototyping alone. I came up with four of the different rules for the game, and I even designed a level!
The atoms that make up the inputs and outputs of the game are little nodes. They'll basically be some shape (probably made distinguishable by color), and they can be connected together by connectors to form more complex structures. The connectors are what give the game depth. There are different types of connectors. I'll explain two of them here.
The first connector looks like this: ^
The second connector looks like this: ->
Anywhere in the play space, you can construct machines that will either add or remove these connectors. Here are diagrams of the machines:
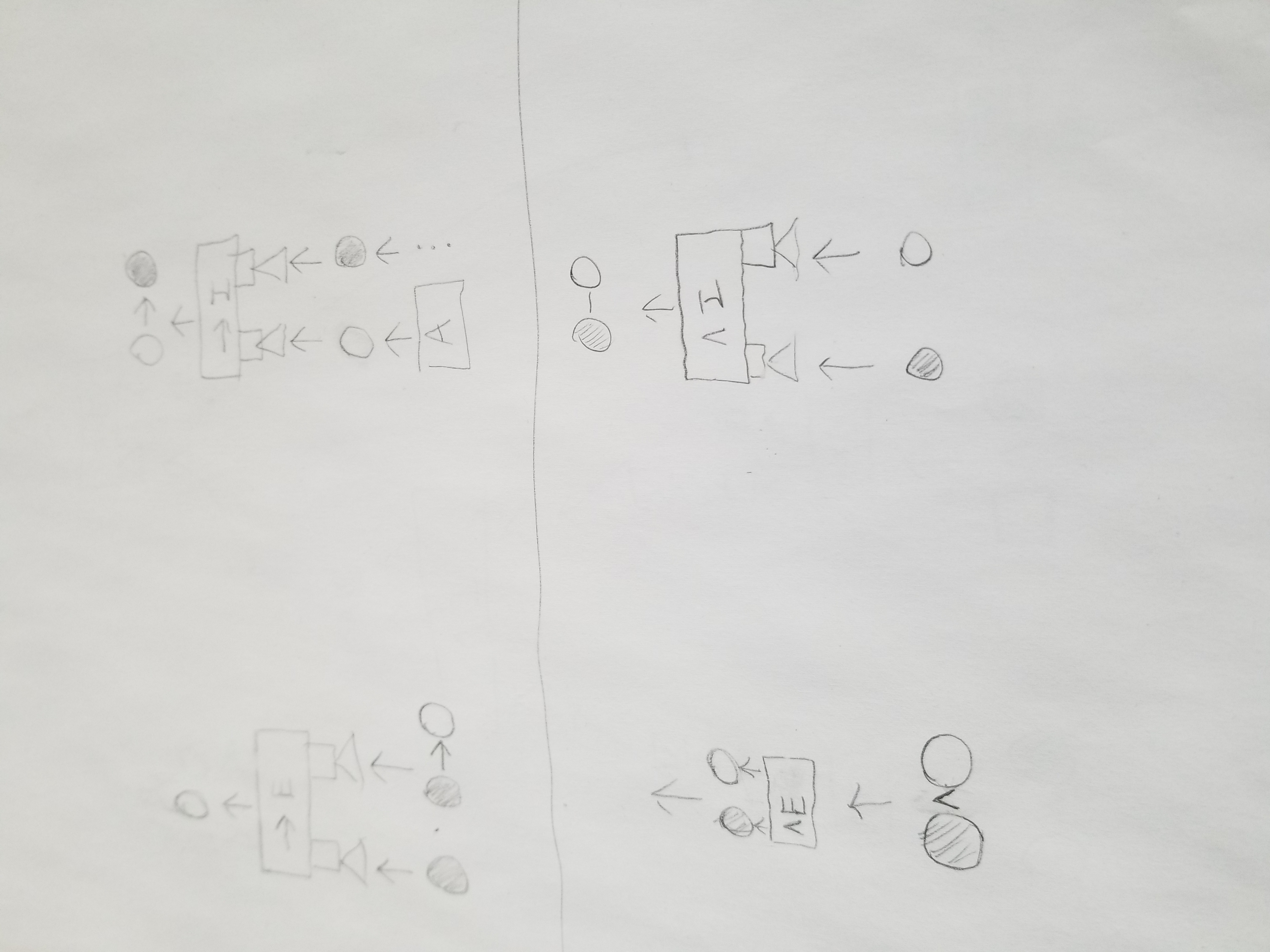
The ->E machine removes the -> connector, while the ->I machine introduces it (I'll probably just change the names of the machines to symbols, to make it more user-friendly. This is just a prototype). A similar story is told for the ^ connector. We can see that each connector behaves differently. The "A" machine is capable of introducing any structure you like, no matter what it is or what the connectors are. However, it's not completely restriction-free. Any structure introduced by the "A" machine has to be destroyed before the final output is processed or the player will fail the puzzle (there are some other, more subtle restrictions on the "A" machine, but this description is already getting rather wordy - it'll make more sense when the game is playable).
After I introduced those four machines, I made my first puzzle. Here it is, solution and all. The inputs are shown at the bottom, while the output is the structure at the very top:

Don't worry about the "X" machine. It won't be in the game. I just used it to denote that I wasn't going to use those nodes. Additionally, note the structure at the bottom-right. The first half of the structure has a box around it. When a sub-structure has a box around it, everything inside the box is treated as a single node.
So, that's it for this week. I hope you enjoyed looking at my paper prototype and reading about the not-so-simple rules of my new game! Honestly, I'm a little worried about this one. I only have a month to pull off a demo. If I can get even one level working, I'll consider it a victory. Keep in mind I also have to balance the development of this game with the updates to POLYPAINT. We'll see how things go, but I'm already almost a week into May and all I have so far is a paper prototype. I'm feeling a little pressed for time, but I believe in myself! See ya next week!
<= Back